Il existe plusieurs sortes de diode, il y a la diode dite normale, il y a  également des diode schotsky et des diodes zenner, les diodes zenners ont comme particularités d'avoir une caractéristique en inverse. En effet les diodes zenners ont un tension d'avalanche : en inverse la diode peut être assimile à une source de tension.

les équations internes d'une zenner sont :

• 1° la zenner est en direct quand id>0 et alors Vd=0.
• 2° la zenner  est bloquée quand -Vz<Vd<0  et alors Id=0.
• 3° la zenner est en inverse quand Id<0 et là VD=-Vz.

en conclusion la caractéristique interne d'une zenner est :

caractéristique non disponible".

La zenner est souvent utilisé pour deux raisons:

• la première c'est en source de tension ,on fait circuler un courant en inverse et la zenner à donc une tension  -Vz (ou tension d'avalanche de la diode)
• la seconde c'est l’écrêtage .

Prenons le schéma suivant :

"schéma non disponible"

établissons les équations externes :

si la Zenner conduit en direct alors Vd(t)=0 alors :

la diode est en direct si id(t) >0 et donc Rid(t)>0 donc

Donc finalement quand

Si la zenner est bloquée alors

elle est bloquée si -Vz<vd(t)<0

or d'après les équations externes :

On injecte les deux equations précédente :

d'où

si la zener est en inverse on peut écrire :

elle est en inverse quand Id <0 donc

Nous pouvons donc faire la représentation suivante

On remarque que la tension est redressée la valeur moyenne augmente de E et est écrêtée, cela permet notamment d’éviter les surtensions (par exemple les surtensions apparaissant aux bornes des bobines )

Ici pour plus de simplicité  on va raisonner sur le fait que le courant descend les potentiels c'est à dire que le courant part du "+" et se dirige vers le "-" et que le courant ne peut traverser une diode quand celle ci ce présente mal.

redressement double alternance

e(t) est positive pour 0<t<pi.

si e(t) >0 VD1 et VD3  serait en direct  (car la tension à leurs bornes est positive) alors que VD2 et VD4 serait en inverse (la tension à leurs bornes serait négative).

on va donc déterminer l'équation de VD4 (VD2 serait identique)

en écrivant la maille on peut dire que :

redressement double alternance

e(t) est négative pour 0<t<pi.

Si e(t)<0 VD2 et VD4  serait en direct  (car la tension à leurs bornes est positive) alors que VD1 et VD3 serait en inverse (la tension a leurs bornes serait négative).

On va donc déterminer l'équation de VD3 (VD1 serait identique)

On écrit à nouveau  la maille et on trouve :

on pourrait donc faire le schéma équivalent qui serait le "jumeau du précédent".

le pont de graetz est le procédé le plus utilisé (car le moins coûteux), il existe cependant d'autre procédé comme celui du transfo à point milieu nous n'allons pas nous attarder sur ce système car il nécessite un transfo et donc cela décourage les constructeurs (vu le prix des transfos...).

"schéma non disponible"

Afin d'avoir le meilleur redressement possible on met un condensateur en parallèle sur la charge pour que la tension soit lissé car la valeur moyenne du signal se retrouve au borne du condensateur donc au borne de la charge.

physiquement le condo agit comme une réserve d'énergie, c'est a dire que lorsque la tension est inférieure à la tension moyenne ,le condo fournit "l'énergie "manquante" et si la tension est supérieure à la tension moyenne le condensateur prend le "surplu".

voici un schéma classique de redressement secteur :

"schéma non disponible"

Considérons le schéma suivant:

redressement simple alternance

On doit établir les équations internes et externes:

• Équations interne (c'est à dire propre à la diode). Ces équations traduisent les caractéristiques que l’on a linéarisée, si on prend le modèle de la diode idéale on obtient :
  
  La diode est bloquée : Id =0 si Vd<0
  La diode conduit vd=0 si ID>0
  
  
• Équation interne : c'est l’équation de la maille (ici il n'y en a qu'une) en utilisant obligatoirement comme variable Vd et Id ; ici on a :
  
  
  e(t) = Vsin (t) = Vd(t) + Vr(t) = Vr(t) = Rid(t).
  
  
  Cette équation externe (externe au composants) écrit donc :
  
  
  Vsin(t)=Vd + Rid(t).
  Cette équation est valable quel que soit l’état de la diode !!!
  
  

Pour déterminer les équations, on va supposer la diode dans un certain état et pour cet état et écrire l’équation externe en prenant légalité des équations interne. Ici on distingue  2 cas :

• la diode est bloquée.
  
  
  Id=0   => e(t)=Vsin (t) =Vd (t) +R * 0
• la diode conduit
  
  
  Si la diode conduit VD(t)=0  => e(t)= Vsin (t) =0 +Rid(t).
  
  
• Étape final : il faut maintenant savoir pour quelle valeur du temps la diode sera effectivement conductrice ou bloquée. Pour cela on applique les 2  règles suivantes :
  • une diode est bloquée si la tension a ses bornes est positive (Vd<0)
  • Une diode est conductrice si le courant qui la traverse est positif Id<0.

Donc pour notre cas présent :

• quand la diode est bloquée Vd(t) = e(t) => elle sera bloquée pour Vd(t) =e(t) <0 donc pi<t<2pi
• quand la diode conduit Vr =Rid=e(t) donc elle conduit si Id= e(t)/r >0  => 0<t<pi

Remarque: nous aurions pu éviter cette dernière étape en effet nous savons qu'une diode n'a que deux état possible, donc si la diode est bloquée de 0 a t elle sera forcement conductrice le reste de la période : de t à T (T est la période du signal périodique).

Une diode est une association de deux semi-conducteurs, ce n'est en fait qu'une jonction PN, son utilité est diverse : on l'utilise pour le redressement ,pour écrêter des signaux (faire en sorte que la valeur ne dépasse pas un certain seuil), pour réguler des tensions (pour éviter des variations brusques de tension qui pourraient endommagées les circuits) et même pour les DELs (diode électroluminescentes) ou LEDs en anglais (figure ci dessous). Une diode est TOUJOURS polarisée ,c'est a dire qu'elle réagit différemment si elle est branchée dans un sens ou dans un autre.

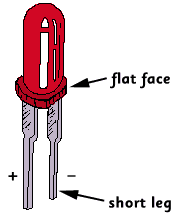
Diode

1°Valeur moyenne :

"formule non disponible"

Xmoy représente la surface du signal x(t).

remarque : la valeur moyenne du courant variable i(t) est égale a l’intensité que doit avoir un courant continu pour transporter la même quantité d’électricité pendant un même intervalle de temps.

2°valeur efficace

"formule non disponible"

remarque : l’intensité efficace d'un courant i(T) est égale a l'intensité d'un courant continu qui produirait le même effet joule pendant la même durée dans le même résistance.

3° Facteur de forme :

Le facteur de forme est égal au quotient de la valeur efficace d'un signal par la valeur moyenne de ce même signal.
"formule non disponible"

Le facteur de forme renseigne sur la qualité du redressement. Au plus F se rapproche de 1 (cas d'un signal constant) et meilleur est le redressement. Par exemple on remarquera dans le tableau ci dessous que le redressement simple alternance (RSA) est moins bon que le redressement double alternance.

"tableau non disponible"

Un redressement idéal serait un système tel que si on lui applique un signal sinusoïdal, on aurait un signal constant en sortie.

LES SEMIS-CONDUCTEURS

Les matières les plus généralement employées sont le silicium et le germanium dans lesquels des impuretés ont été présentées. Dans un semi-conducteurs de type N, il y a un excès d'électrons libres, ou charges négatives, tandis que dans un semi-conducteurs de type P, il y a une insuffisance d ' électrons et donc un excès des charges positives. Les transistors et les diodes sont des composants clés des circuit intégrés et sont utilisés dans beaucoup d'applications : les récepteurs radio, ordinateurs, électroniques diverse, et instrumentation de contrôle automatique (par exemple, dans l'aéronautique et les missiles téléguidés). Depuis l'invention (annoncée en 1948) du transistor par les physiciens américains John BARDEEN, Walter H. Brattain, et William Shockley, beaucoup de types ont été conçus. Ceux-ci sont généralement classés en tant qu'effet bipolaire ou de champs. Un transistor bipolaire se compose de trois couches : * une couche haute et une couche basse, appelées l'émetteur et le collecteur, et qui sont d'un certain type de conductivité. * ainsi qu'une couche moyenne, appelée base. Les surfaces de séparation entre les diffèrents types de conducteurs s'appellent les jonctions PN. Les électrons traversent les jonctions d'une couche vers l'autre. L'action du transistor n'est réalisée que si les potentiels électriques sur les segments sont correctement polarisés, un petit courant entre l'émetteur et la base engendre un grand courant entre l'émetteur et le collecteur, produisant de ce fait une l'amplification. les fonctions d'un transistor à effet de champ sont semblables sauf que l'écoulement d'électron est modulées par un champ électrique externe. Dans un transistor à effet de champ (JFET), le champ électrique de contrôle est produit par une jonction PN polarisée en inverse.

[th de Kirchoff] [th de superposition] [th de thevenin] [th de norton] [équivalence norton thevenin] [th de kennely]

Ce sont deux lois fondamentales des circuits électriques aussi bien pour des circuits linéaires que pour des circuits non-linéaires.

La loi des noeuds :

La somme algébrique des courants arrivant à un noeud est nulle.

loi de kirshoff- loi des noeuds

La loi des noeuds nous permet d'affirmer que

i1+i2+i3-i4=0

Remarques : les courants peuvent être positifs ou négatifs selon qu'ils arrivent à un noeud ou qu'ils en partent.

La loi des mailles :

La somme algébrique des tensions le long d'une maille fermée est nulle.

loi de kirshoff- loi des mailles

On peut donc écrire que : u1+u2+u4+u5=0
Remarques :Les tensions peuvent être positifs ou négatifs selon quon prend la maille dans un sens ou dans un autre.

Dans un circuit linéaire, le courant produit par plusieurs sources de courants indépendantes est égale à la somme des courants produits par chaque sources prises isolement.

Considérons le schéma électrique suivant et tentons de déterminer quel est le courant dans chaque branches :

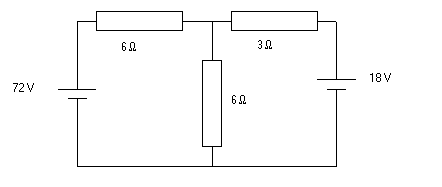
Théorème de superposition

D'après le théorème énoncé ci dessus, le courant dans chaque branche résulte du courant traversant cette branche si la source de tension E1 (72 v) agissait seule et de celui si E2 (18 v) agissait seule. Étudions donc les deux cas :

• Si E1 agit seule on a le schéma électrique suivant :

Shéma si E1 agit seule

On peut alors simplifier ce schéma de la manière suivante en appliquant les règles vues au chapitre "les résistances en parallèles "

Req = (R1 *R2 ) / (R1 + R2 )

donc

Req = (6*3) / (6+3 )= 2 ohms

Shéma simplifié si E1 agit seule

En appliquant la loi d'ohm on trouve le courant débité par E1 :

I = U / R donc I =72 / (6+ 2 )=9 A

On applique donc le pont diviseur en courant pour  trouver le courant dans chacune des branches du schéma précèdent.

Dans la résistance de 3 ohms circule un courant de (9 * (1/3))/(1/2) = 6 A

Dans celle de 6 ohms circule un courant de (9*(1/6))/(1/2 ) = 3 A

• Si E2 agit seule on obtient le schéma suivant :

Shéma si E2 agit seule

Que l'on peut également simplifier de la même manière que précédemment :

Shéma simplifié si E2 agit seule

En résumé :

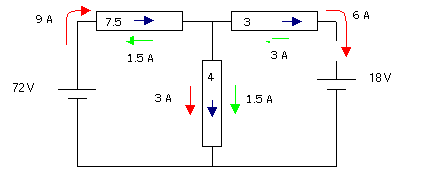
Shéma final

En bleu figure le courant réel, en rouge, celui si E1 agissait seule et en vert si E2 agissait seule

Tout sous réseau d'un réseau peut être remplacé par un générateur de tension et une résistance en série avec ce générateur.

Comment trouver le générateur de thevenin ?:

• 1° Isoler le réseau (c'est à dire retirer tous les éléments qui ne font pas partis du sous réseau pour lequel on désire  connaître le générateur de Thevenin ).
• 2° Remplacer les sources de tension par des courts circuits et les sources de courant par des circuits ouverts .
• 3° Calculer la résistance de thevenin (la résistance équivalente du circuit).
• 4° Rebrancher les sources (annuler l'étape 2).
• 5° Calculer la tension de thevenin (tension équivalente entre les deux bornes du réseau pour lequel on cherche le générateur de Thevenin).

Tout sous réseau d'un réseau peut être remplacé par un générateur de courant et une résistance en parallèle  avec ce générateur.

Comment trouver le générateur de Norton ? :

• 1° Pour déterminer la résistance, on annule toutes les sources du réseau 1 et on détermine la résistance équivalente vu des deux bornes du réseau.
• 2° Pour calculer le générateur de courant équivalent il suffit de calculer le courant de court-circuit circulant entre les deux bornes du réseau.

Dans bien des cas, le générateur de Norton est plus complexe à déterminer que le générateur de Thevenin, c'est pourquoi il est bien souvent préférable de calculer le générateur de thevenin et de le transposer en générateur de Norton. Pour cela on applique la méthode de la transposition des sources :

transposition des sources

Si on connaît la résistance de thevenin Rth, on en déduit la résistance de thevenin Gn  par la relation suivante :

Gn = 1/Rth

De même, si on connaît le générateur de thevenin Eth on en déduit le générateur de Norton In:

In  =Eth/Rth

Le théorème de Kennely permet de passer d'un schéma en triangle à un schéma en étoile et inversement :

Théoreme de kennely

Nous ne nous attarderons pas sur la démonstration mathématique mais allons directement nous intéresser à la formule finale :

• Ra = (Rab * Rac)/somme
• Rb = (Rba * Rbc)/somme
• Rc = (Rca * Rcb)/somme

Formule réciproque :

à partir d'un schéma en étoile on peut également  trouver le schéma en triangle correspondant avec les formules suivantes:

• Rac = (Ra * Rb + Ra * Rc + Rb * Rc)/somme.
• Rab = (Ra * Rb + Ra * Rc + Rb * Rc)/somme
• Rbc = (Ra * Rb + Ra * Rc + Rb * Rc)/somme

[th de Kirchoff] [th de superposition] [th de thevenin] [th de norton] [équivalence norton thevenin] [th de kennely]

Ce sont deux lois fondamentales des circuits électriques aussi bien pour des circuits linéaires que pour des circuits non-linéaires.

La loi des noeuds :

La somme algébrique des courants arrivant à un noeud est nulle.

loi de kirshoff- loi des noeuds

La loi des noeuds nous permet d'affirmer que

i1+i2+i3-i4=0

Remarques : les courants peuvent être positifs ou négatifs selon qu'ils arrivent à un noeud ou qu'ils en partent.

La loi des mailles :

La somme algébrique des tensions le long d'une maille fermée est nulle.

loi de kirshoff- loi des mailles

On peut donc écrire que : u1+u2+u4+u5=0
Remarques :Les tensions peuvent être positifs ou négatifs selon quon prend la maille dans un sens ou dans un autre.

Dans un circuit linéaire, le courant produit par plusieurs sources de courants indépendantes est égale à la somme des courants produits par chaque sources prises isolement.

Considérons le schéma électrique suivant et tentons de déterminer quel est le courant dans chaque branches :

Théorème de superposition

D'après le théorème énoncé ci dessus, le courant dans chaque branche résulte du courant traversant cette branche si la source de tension E1 (72 v) agissait seule et de celui si E2 (18 v) agissait seule. Étudions donc les deux cas :

• Si E1 agit seule on a le schéma électrique suivant :

Shéma si E1 agit seule

On peut alors simplifier ce schéma de la manière suivante en appliquant les règles vues au chapitre "les résistances en parallèles "

Req = (R1 *R2 ) / (R1 + R2 )

donc

Req = (6*3) / (6+3 )= 2 ohms

Shéma simplifié si E1 agit seule

En appliquant la loi d'ohm on trouve le courant débité par E1 :

I = U / R donc I =72 / (6+ 2 )=9 A

On applique donc le pont diviseur en courant pour  trouver le courant dans chacune des branches du schéma précèdent.

Dans la résistance de 3 ohms circule un courant de (9 * (1/3))/(1/2) = 6 A

Dans celle de 6 ohms circule un courant de (9*(1/6))/(1/2 ) = 3 A

• Si E2 agit seule on obtient le schéma suivant :

Shéma si E2 agit seule

Que l'on peut également simplifier de la même manière que précédemment :

Shéma simplifié si E2 agit seule

En résumé :

Shéma final

En bleu figure le courant réel, en rouge, celui si E1 agissait seule et en vert si E2 agissait seule

Tout sous réseau d'un réseau peut être remplacé par un générateur de tension et une résistance en série avec ce générateur.

Comment trouver le générateur de thevenin ?:

• 1° Isoler le réseau (c'est à dire retirer tous les éléments qui ne font pas partis du sous réseau pour lequel on désire  connaître le générateur de Thevenin ).
• 2° Remplacer les sources de tension par des courts circuits et les sources de courant par des circuits ouverts .
• 3° Calculer la résistance de thevenin (la résistance équivalente du circuit).
• 4° Rebrancher les sources (annuler l'étape 2).
• 5° Calculer la tension de thevenin (tension équivalente entre les deux bornes du réseau pour lequel on cherche le générateur de Thevenin).

Tout sous réseau d'un réseau peut être remplacé par un générateur de courant et une résistance en parallèle  avec ce générateur.

Comment trouver le générateur de Norton ? :

• 1° Pour déterminer la résistance, on annule toutes les sources du réseau 1 et on détermine la résistance équivalente vu des deux bornes du réseau.
• 2° Pour calculer le générateur de courant équivalent il suffit de calculer le courant de court-circuit circulant entre les deux bornes du réseau.

Dans bien des cas, le générateur de Norton est plus complexe à déterminer que le générateur de Thevenin, c'est pourquoi il est bien souvent préférable de calculer le générateur de thevenin et de le transposer en générateur de Norton. Pour cela on applique la méthode de la transposition des sources :

transposition des sources

Si on connaît la résistance de thevenin Rth, on en déduit la résistance de thevenin Gn  par la relation suivante :

Gn = 1/Rth

De même, si on connaît le générateur de thevenin Eth on en déduit le générateur de Norton In:

In  =Eth/Rth

Le théorème de Kennely permet de passer d'un schéma en triangle à un schéma en étoile et inversement :

Théoreme de kennely

Nous ne nous attarderons pas sur la démonstration mathématique mais allons directement nous intéresser à la formule finale :

• Ra = (Rab * Rac)/somme
• Rb = (Rba * Rbc)/somme
• Rc = (Rca * Rcb)/somme

Formule réciproque :

à partir d'un schéma en étoile on peut également  trouver le schéma en triangle correspondant avec les formules suivantes:

• Rac = (Ra * Rb + Ra * Rc + Rb * Rc)/somme.
• Rab = (Ra * Rb + Ra * Rc + Rb * Rc)/somme
• Rbc = (Ra * Rb + Ra * Rc + Rb * Rc)/somme

Les composants Electroniques

Definition:

Un Composant électronique est un élément destiné à être assemblé avec d'autres afin de réaliser un circuit electronique.

on distingue deux types de composants :

- composants actifs

- composants passifs

Un composant actif est un composant électronique qui permet d'augmenter la puissance d'un signal (tension, courant, ou les deux).

comme composants actifs nous pouvons citer:

les circuits integres

les transistors

les diodes

quartz

les thyristors

comme composants passifs nous pouvons citer:

les condensateurs

les resistances

les potentiometres

les inductences

etc...................................